Published on JAN 21 2025 by James Smith

Got somewhere by map? Thank Dijkstra's algorithm

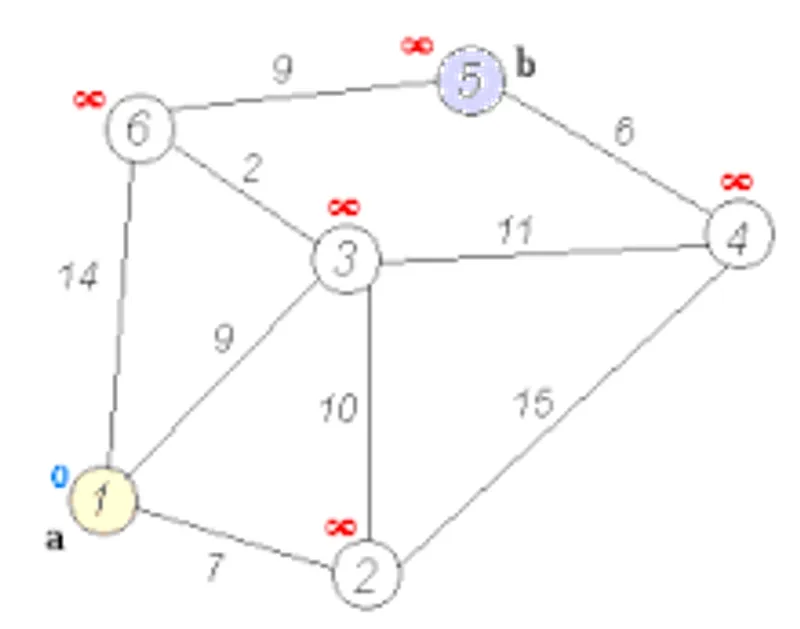
Dijkstra’s algorithm is a way to find the shortest path between points, often called nodes, on a map or network. Imagine you’re planning a road trip. You have a map showing various cities (nodes) and the roads connecting them, with the distances labeled. You want to find the quickest route from your home city to a destination city. Dijkstra’s algorithm helps do exactly that—it calculates the shortest path to get where you’re going while passing through the least amount of distance or cost.

The process starts with your home city. The algorithm looks at all the neighboring cities and figures out which one is closest. From there, it moves to the next nearest city and repeats the process, always choosing the shortest route at each step. It keeps track of the total distance it’s traveled as it goes, ensuring that it’s always working toward the shortest overall path. Importantly, the algorithm doesn’t stop until it has evaluated all possible routes, so even if the shortest path takes a less obvious route through multiple cities, Dijkstra’s method will find it.

In real-world terms, Dijkstra’s algorithm has countless practical uses. One of the most obvious applications is in GPS navigation systems like Google Maps. When you input a destination, the system uses this algorithm (or similar ones) to calculate the shortest or fastest route by evaluating road distances, traffic conditions, and other factors. The algorithm ensures that you’re directed on a route that minimizes travel time or distance.

Beyond navigation, the algorithm is used in computer networks. For example, when data is sent across the internet, it needs to travel through various routers and connections. Dijkstra’s algorithm helps determine the most efficient path for the data to travel, ensuring it reaches its destination as quickly as possible. This is crucial for maintaining the speed and reliability of online communication.

Another real-world application is in transportation planning. Airlines, for instance, use similar algorithms to determine the most efficient flight routes, considering factors like distance, fuel consumption, and air traffic. Similarly, logistics companies like UPS or FedEx use it to optimize delivery routes, ensuring packages are delivered efficiently while minimizing costs.

Dijkstra’s algorithm is also used in gaming, where characters or units need to navigate through a virtual world. The algorithm helps them find the shortest or most logical path between two points in the game environment, making their movements appear more natural and intelligent.

In essence, Dijkstra’s algorithm is like a decision-making tool for finding the best path in any situation where there are multiple options and costs associated with them. Whether it’s guiding you on a road trip, delivering packages, or helping data travel across the internet, its practicality and efficiency make it an essential tool in many areas of our modern world.

Graph Theory

Dijkstra’s algorithm is deeply rooted in graph theory, a branch of mathematics that studies relationships between objects. In this context, the map or network can be thought of as a graph, with cities or points represented as nodes and the roads connecting them as edges. Each edge has a weight, which might represent the distance, cost, or time required to travel between nodes. Dijkstra’s algorithm operates on this graph by systematically exploring paths, starting from a source node and calculating the shortest distance to all other nodes. This graph-theoretic foundation makes the algorithm versatile, as it can be applied to any problem that can be modeled as a graph, whether it’s a physical road network, a data communication system, or even the connections between characters in a social network. By leveraging the properties of graphs, Dijkstra’s algorithm ensures an efficient and mathematically sound way to find optimal paths in complex systems.

Written by James Smith